Ilhan Kaya, Kevin P. Thompson, and Jannick P. Rolland
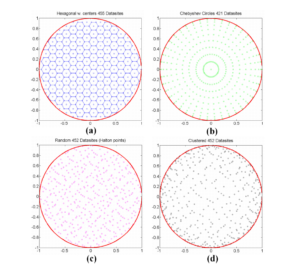
With the recent emergence of slow-servo diamond turning, optical designs with surfaces that are not intrinsically rotationally symmetric can be manufactured. In this paper, we demonstrate some important limitations to Zernike polynomial representation of optical surfaces in describing the evolving freeform surface descriptions that are effective for optical design and encountered during optical fabrication. Specifically, we show that the ray grids commonly used in sampling a freeform surface to form a database from which to perform a φ-polynomial fit is limiting the efficacy of computation. We show an edge-clustered fitting grid that effectively suppresses the edge ringing that arises as the polynomial adapts to the fully nonsymmetric features of the surface.