Tell me simply: Whether you speak with an optical designer or a fabricator, a different viewpoint may emerge on what may be considered precisely freeform.
In simple terms (and perhaps too simple), a freeform surface is defined as a surface whose surface shape lacks translational or rotational symmetry.
Tell me the details: Freeform optics involve optical designs with at least one freeform surface which, according to the ISO standard 17450-1:2011, has no translational or rotational symmetry about axes normal to the mean plane. Nonimaging and illumination optics have leveraged freeform surfaces since at least the 1990s [1]. Integration of freeform optics and surfaces into imaging systems remains as a major challenge. However, the new degrees of freedom introduced by freeform optics designs are the driver to overcoming these challenges. Freeform optics unconstrain optical design, improve performance, and reduce part count and package size.
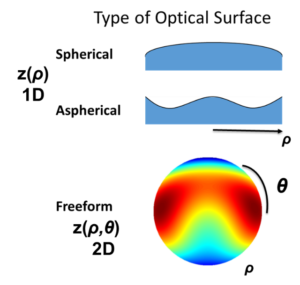Traditional optical surfaces are spherical (a plane being the special case with a radius of curvature going to infinity) or, since the 1902 Ernst Abbe patent at Carl Zeiss Corporation, rotationally symmetric aspherical surfaces [2]. Since 2007, aspherical surfaces have seen a mathematical transformation through the pioneering work of Gregory Forbes in developing 1D Q-polynomials, an orthonormal basis in slope to describe aspherical surfaces [3]. This new description departs from simple monomials and has been shown to provide benefits in the manufacturability of aspherical surfaces.
Anamorphic optics involves optical designs with a combination of spherical, aspherical and toroidal surfaces – the last of which are the launching point for freeform optics [4-5]. Historically, XY-polynomials were the first type of polynomials used for low-order freeform surfaces [6]. These polynomials remain common surface descriptors of freeform surfaces and enable, for example, variable optical functions when used in pairs [7-10]. However their lack of orthogonality renders them less desirable than their orthogonal counterparts for highly corrected imaging systems. Mathematically, freeform surfaces may be best defined through either local descriptions (such as radial basis functions [11] and non-uniform rational B-splines [12]) or global descriptions such as orthogonal polynomials [13-17]. Zernike polynomials, which are orthogonal in sag, have shown great promise in optical design for manufacture [18], especially when combined with the emerging theory of aberrations for freeform surfaces [19-20]. An open question is whether or not the Q-polynomials developed by Forbes that are orthogonal in gradient [15] will come to compete with Zernike polynomials when designing for manufacture [21].
Manufacturing and metrology must keep pace with design in order to realize the full potential of freeform optics [22]. Traditional two degree of freedom manufacturing processes such as grinding, polishing, and ultraprecision turning are not capable of manufacturing freeform surfaces. Higher degree of freedom processes such as coordinated axis diamond turning [23], diamond milling [24] and deterministic micro-grinding and polishing [25] are required to generate arbitrary freeform surfaces. However, the additional degrees of freedom intrinsically increase the positioning uncertainty and make it challenging to simultaneous meet optical designers’ requirements for optical form, mid-spatial frequencies, and surface micro-roughness. Significant additional challenges remain in the metrology of freeform surfaces at this level as the metrology platforms often have uncertainties that are comparable to the manufacturing platforms [22].
[1] K.P. Thompson, M. Benitez, and J.P. Rolland, “Freeform Optical Surfaces: Report from OSA 1st Incubator Meeting”, Optics & Photonics News 23(9), 32-37 (2012)
[2] E. Abbe, “Lens system,” U.S. Patent 697,959 (Apr. 1902)
[3] G. W. Forbes, “Shape specification for axially symmetric optical surfaces,” Opt. Express 15(8), 5218–5226 (2007)
[4] Kevin P. Thompson and Jannick P. Rolland, “Freeform Optical Surfaces: A Revolution in Imaging Optical Design” Optics & Photonics News 23(6), 30-35 (2012)
[5] J. P. Rolland and K.P. Thompson, “Freeform optics: Evolution? No, revolution!, SPIE Newsroom 19 July (2012)
[6] W. T. Plummer, J. G. Baker, and J. Van Tassell, “Photographic optical systems with nonrotational aspheric surfaces,” Appl. Opt. 38(16), 3572–3592 (1999).
[7] Alvarez, L. W., “Two-element variable-power spherical lens,” U. S. Patent No. 3,305,294 (1967).
[8] Palusinski, I. A., Sasian, J. M., and Greivenkamp, J. E., “Lateral-shift variable aberration generators,” Appl. Opt. 38, 86–90 (1999).
[9] P. J. Smilie, B. S. Dutterer, J. L. Lineberger, M. A. Davies, T. J. Suleski, “Design and characterization of an infrared Alvarez Lens”, Optical Engineering 51(1), 013006 (2012).
[10] P. J. Smilie, T. J. Suleski, Variable-diameter refractive beam shaping with freeform optical surfaces, Optics Letters, 36(21): 4170-4172 (2011)
[11] O. Cakmakci, B. Moore, H. Foroosh, and J. P. Rolland, “Optimal local shape description for rotationally nonsymmetric optical surface design and analysis,” Opt. Express 16(3), 1583–1589 (2008)
[12] M. P. Chrisp and B. Primeau, “Imaging with NURBS freeform surfaces,” in Imaging and Applied Optics 2015, OSA Technical Digest (online) (OSA, 2015), FW2B.1.
[13] G. W. Forbes, “Robust and fast computation for the polynomials of optics,” Opt. Express 18(13), 13851–13862 (2010)
[14] I. Kaya, K. P. Thompson, and J. P. Rolland, “Edge clustered fitting grids for polynomial characterization of freeform optical surfaces,” Opt. Express 19(27), 26962–26974 (2011)
[15] G. W. Forbes, “Characterizing the shape of freeform optics,” Opt. Express 20(3), 2483–2499 (2012)
[16] I. Kaya, K. P. Thompson and J. P. Rolland, “Comparative assessment of freeform polynomials as optical surface descriptions,” Opt. Express 20(20), 22684–22691 (2012)
[17]. Kaya and J. P. Rolland, “Hybrid RBF and local φ-polynomial freeform surfaces” Adv. Opt. Techn. 2(1), 81-88 (2013)
[18] K. Fuerschbach, J. P. Rolland, and K. P. Thompson, “A new family of optical systems employing φ-polynomial surfaces,” Opt. Express 19(22), 21919 (2011)
[19] K. Fuerschbach, J. P. Rolland, and K. P. Thompson, “Theory of aberration fields for general optical systems with freeform surfaces,” Opt. Express 22(22), 26585–26606 (2014)
[20] A. Bauer and J. P. Rolland, “Design of a freeform electronic viewfinder
coupled to aberration fields of freeform optics, “ Opt. Express 23(22), 28142-28153 (2015)
[21] N. Takaki and J.P. Rolland, “Mathematical Properties of Describing Freeform Optical
Surfaces with Orthogonal Bases,” OSA Optical design and fabrication congress JW1B.1 (2017)
[22] F.Z. Fang, X.D. Zhang, A. Weckenmann G.X. Zhang C. Evans, Manufacturing and measurement of freeform optics, CIRP Annals – Manufacturing Technology, 62(2):823-846 (2013)
[23] Troutman, J. R., Barnhardt, D., Shultz, J., Owen, J. D., Davies, M. A., Suleski, T. J., Machining and metrology of a chalcogenide glass lens pair, Procedia Manufacturing, 5:669-683 (2016)
[24] J. D. Owen, J. A. Shultz, T. J. Suleski, M. A. Davies, Error correction methodology for ultra-precision three-axis milling of freeform optics, CIRP Annals – Manufacturing Technology, 66(1), in press (2017).
[25] J. L. Ruckman, E. M. Fess, H. M. Pollicove, Deterministic processes for manufacturing conformal (freeform) optical surfaces, Proc. SPIE 4375, Window and Dome Technologies and Materials VII, 108 (2001).